动态树LCT
~ 2025-7-16 16:37:00
简介(抄OIWIKI,看不懂就认真听讲)
Link/Cut Tree 是一种数据结构,我们用它来解决 动态树问题。
Link/Cut Tree 又称 Link-Cut Tree,简称 LCT,但它不叫动态树,动态树是指一类问题。
Splay Tree 是 LCT 的基础,但是 LCT 用的 Splay Tree 和普通的 Splay 在细节处不太一样(进行了一些扩展)。
问题引入
维护一棵树,支持如下操作:
- 修改两点间路径权值。
- 查询两点间路径权值和。
- 修改某点子树权值。
- 查询某点子树权值和。
这是一道树剖模版题。
但是再加一个操作:
- 断开并连接一些边,保证仍是一棵树。
要求在线求出上面的答案。
这就成了动态树问题,可以使用 LCT 求解。
动态树问题
维护一个 森林,支持删除某条边,加入某条边,并保证加边,删边之后仍是森林。我们要维护这个森林的一些信息。
一般的操作有两点连通性,两点路径权值和,连接两点和切断某条边、修改信息等。
从 LCT 的角度回顾一下树链剖分
- 对整棵树按子树大小进行剖分,并重新标号。
- 我们发现重新标号之后,在树上形成了一些以链为单位的连续区间,并且可以用线段树进行区间操作。
转向动态树问题
我们发现我们刚刚讲的树剖是以子树大小作为划分条件。那我们能不能重定义一种剖分,使它更适应我们的动态树问题呢?
考虑动态树问题需要什么链。
由于动态维护一个森林,显然我们希望这个链是我们指定的链,以便利用来求解。
实链剖分
对于一个点连向它所有儿子的边,我们自己选择一条边进行剖分,我们称被选择的边为实边,其他边则为虚边。对于实边,我们称它所连接的儿子为实儿子。对于一条由实边组成的链,我们同样称之为实链。请记住我们选择实链剖分的最重要的原因:它是我们选择的,灵活且可变。正是它的这种灵活可变性,我们采用 Splay Tree 来维护这些实链。
LCT
我们可以简单的把 LCT 理解成用一些 Splay 来维护动态的树链剖分,以期实现动态树上的区间操作。对于每条实链,我们建一个 Splay 来维护整个链区间的信息。
辅助树
我们先来看一看辅助树的一些性质,再通过一张图实际了解一下辅助树的具体结构。
在本文里,你可以认为一些 Splay 构成了一个辅助树,每棵辅助树维护的是一棵树,一些辅助树构成了 LCT,其维护的是整个森林。
- 辅助树由多棵 Splay 组成,每棵 Splay 维护原树中的一条路径,且中序遍历这棵 Splay 得到的点序列,从前到后对应原树「从上到下」的一条路径。
- 原树每个节点与辅助树的 Splay 节点一一对应。
- 辅助树的各棵 Splay 之间并不是独立的。每棵 Splay 的根节点的父亲节点本应是空,但在 LCT 中每棵 Splay 的根节点的父亲节点指向原树中 这条链 的父亲节点(即链最顶端的点的父亲节点)。这类父亲链接与通常 Splay 的父亲链接区别在于儿子认父亲,而父亲不认儿子,对应原树的一条 虚边。因此,每个连通块恰好有一个点的父亲节点为空。
- 由于辅助树的以上性质,我们维护任何操作都不需要维护原树,辅助树可以在任何情况下拿出一个唯一的原树,我们只需要维护辅助树即可。
现在我们有一棵原树,如图所示。(加粗边是实边,虚线边是虚边。)
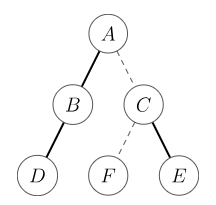
由刚刚的定义,辅助树的结构如图所示。
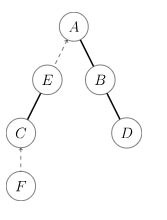
考虑原树和辅助树的结构关系
- 原树中的实链 : 在辅助树中节点都在一棵 Splay 中。
- 原树中的虚链 : 在辅助树中,子节点所在 Splay 的 Father 指向父节点,但是父节点的两个儿子都不指向子节点。
- 注意:原树的根不等于辅助树的根。
- 原树的 Father 指向不等于辅助树的 Father 指向。
- 辅助树是可以在满足辅助树、Splay 的性质下任意换根的。
- 虚实链变换可以轻松在辅助树上完成,这也就是实现了动态维护树链剖分。
以模板题为例讲一下LCT的实现(以下内容不是抄的了)
需要实现的四个操作:
0 x y代表询问从 到 的路径上的点的权值的 和。保证 到 是联通的。1 x y代表连接 到 ,若 到 已经联通则无需连接。2 x y代表删除边 ,不保证边 存在。3 x y代表将点 上的权值变成 。
与splay相比新加入的函数的含义(看不懂请认真听讲)
Access(x)把从根到 的所有点放在一条实链里,使根到 成为一条实路径,并且在同一棵 Splay 里。只有此操作是必须实现的,其他操作视题目而实现。IsRoot(x)判断 是否是所在树的根。Update(x)在Access操作之后,递归地从上到下PushDown更新信息。MakeRoot(x)使 点成为其所在树的根。Link(x, y)在 两点间连一条边。Cut(x, y)把 两点间边删掉。Find(x)找到 所在树的根节点编号。Split(x, y)提取出 间的路径,方便做区间操作。
函数讲解
PushUp()
void pushup(int x)
{
tree[x].res = tree[tree[x].ch[0]].res ^ tree[tree[x].ch[1]].res ^ tree[x].val;
}
PushDown()
void pushdown(int x)
{
if(tree[x].tag){
swap(tree[tree[x].ch[0]].ch[0],tree[tree[x].ch[0]].ch[1]);
swap(tree[tree[x].ch[1]].ch[0],tree[tree[x].ch[1]].ch[1]);
tree[tree[x].ch[0]].tag^=1;
tree[tree[x].ch[1]].tag^=1;
tree[x].tag = 0;
}
}
isroot
//结合定义想象一下如何判断一个节点是不是辅助树的根节点?
int isroot(int x)
{
return tree[tree[x].fa].ch[0]!=x && tree[tree[x].fa].ch[1]!=x;
}
Get()
int Get(int x){
return x == tree[tree[x].fa].ch[1];
}
Splay() && Rotate() && Update(x)
这里 Splay() 和 Rotate() 与 Splay 树的实现有些区别。
void rotate(int x)
{
int y = tree[x].fa,z=tree[y].fa,chk=Get(x);
if(!isroot(y))tree[z].ch[y==tree[z].ch[1]]=x;//思考为什么写前面?
tree[x].fa = z;
tree[y].ch[chk] = tree[x].ch[chk^1];
if(tree[x].ch[chk^1])tree[tree[x].ch[chk^1]].fa = y;
tree[x].ch[chk^1] = y;
tree[y].fa = x;
pushup(y);
pushup(x);
}
void splay(int x)
{
update(x);
while(!isroot(x)){
int y = tree[x].fa;
if(!isroot(y)){
if(Get(y)==Get(x))rotate(y);
else rotate(x);
}
rotate(x);
}
pushup(x);
}
void update(int x)
{
//因为要转上去,所以先从上到下更新一遍
if(!isroot(x))update(tree[x].fa);
pushdown(x);
}
Access()
// Access 是 LCT
// 的核心操作,试想我们像求解一条路径,而这条路径恰好就是我们当前的一棵 Splay,
// 直接调用其信息即可。先来看一下代码,再结合图来看看过程
int access(int x)
{
int y;
for(y=0;x;y=x,x=tree[x].fa){
splay(x);
tree[x].ch[1] = y;
pushup(x);
}
return y;
}
-
我们有这样一棵树,实线为实边,虚线为虚边。
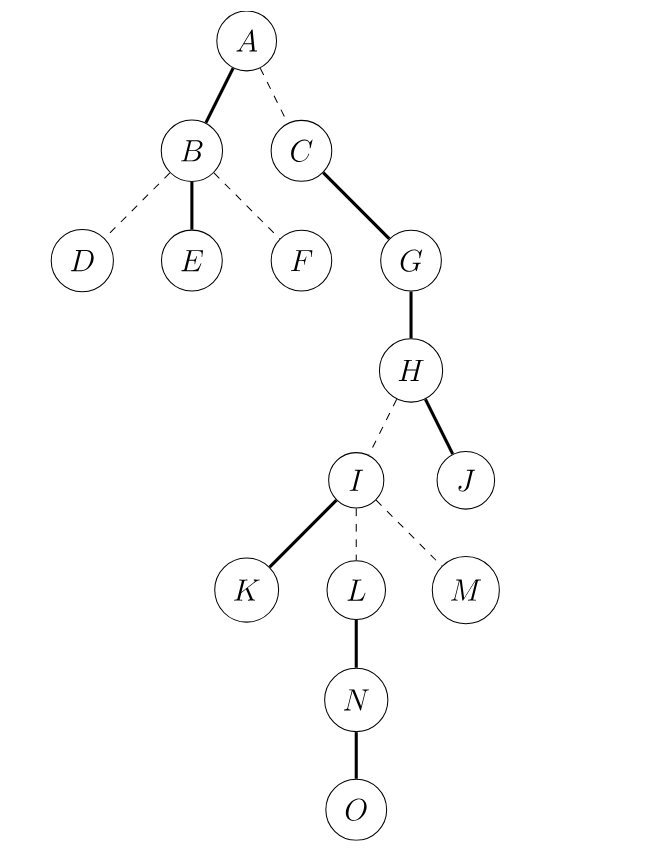
-
它的辅助树可能长成这样(构图方式不同可能 LCT 的结构也不同)。
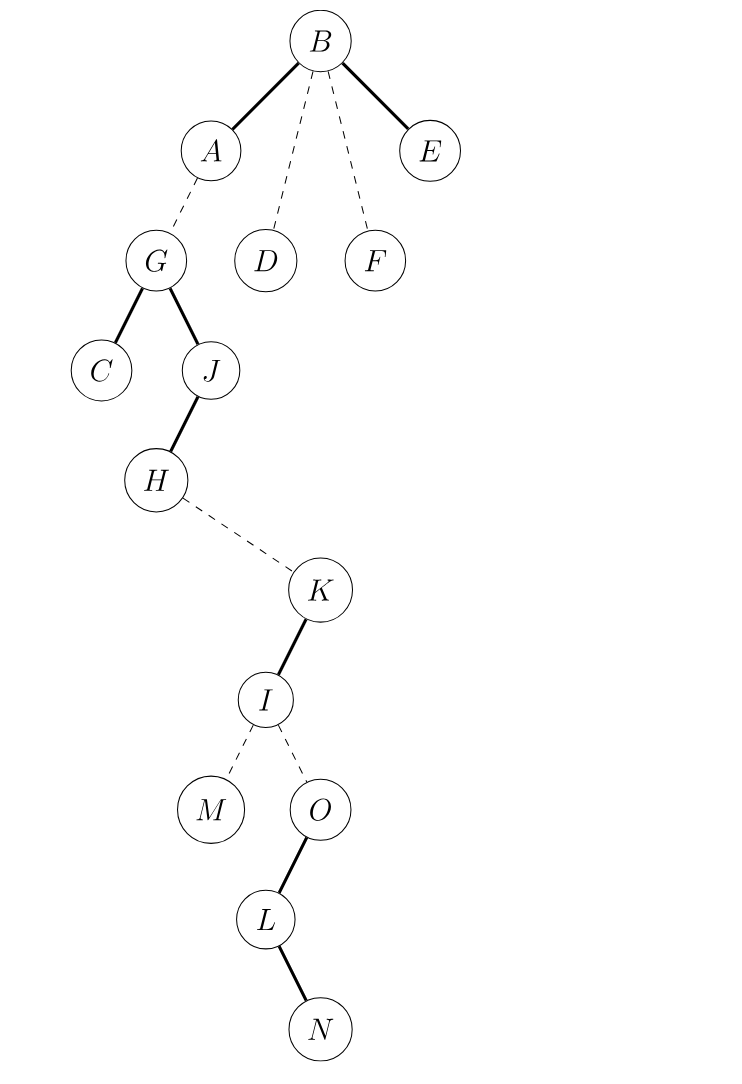
-
现在我们要
Access(N),把 到 路径上的边都变为实边,拉成一棵 Splay。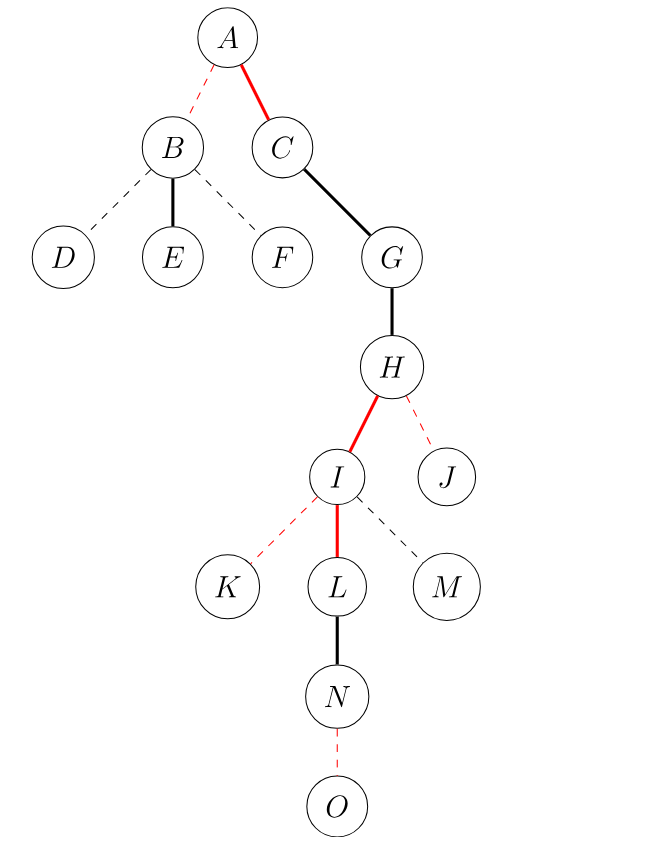
-
实现的方法是从下到上逐步更新 Splay。
-
首先我们要把 旋至当前 Splay 的根。
-
为了保证 AuxTree(辅助树)的性质,原来 到 的实边要更改为虚边。
-
由于认父不认子的性质,我们可以单方面的把 的儿子改为
NULL。 -
于是原来的 AuxTree 就从下图变成了下下图。
-
下一步,我们把 指向的 Father 也旋转到 的 Splay 树根。
-
原来的实边 — 要去掉,这时候我们把 的右儿子指向 ,就得到了 — 这样一棵 Splay。
-
接下来,按照刚刚的操作步骤,由于 的 Father 指向 ,我们把 旋转到他所在 Splay Tree 的根,然后把 的 rs 设为 。
-
之后的树是这样的。
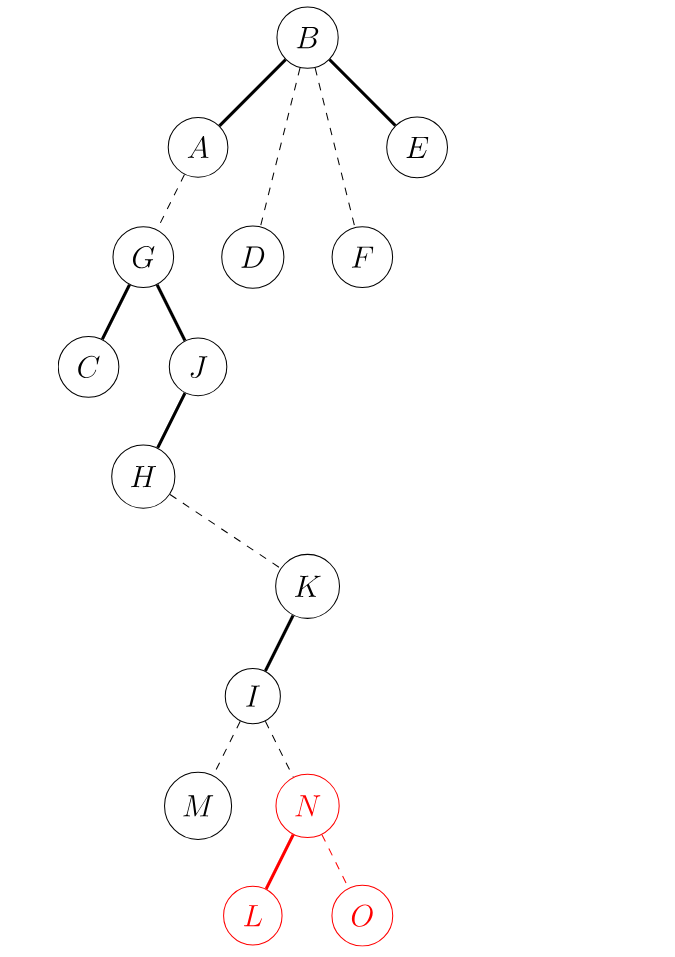
-
同理我们
Splay(A),并把 的右儿子指向 。 -
于是我们得到了这样一棵 AuxTree。并且发现 — 的整个路径已经在同一棵 Splay 中了。
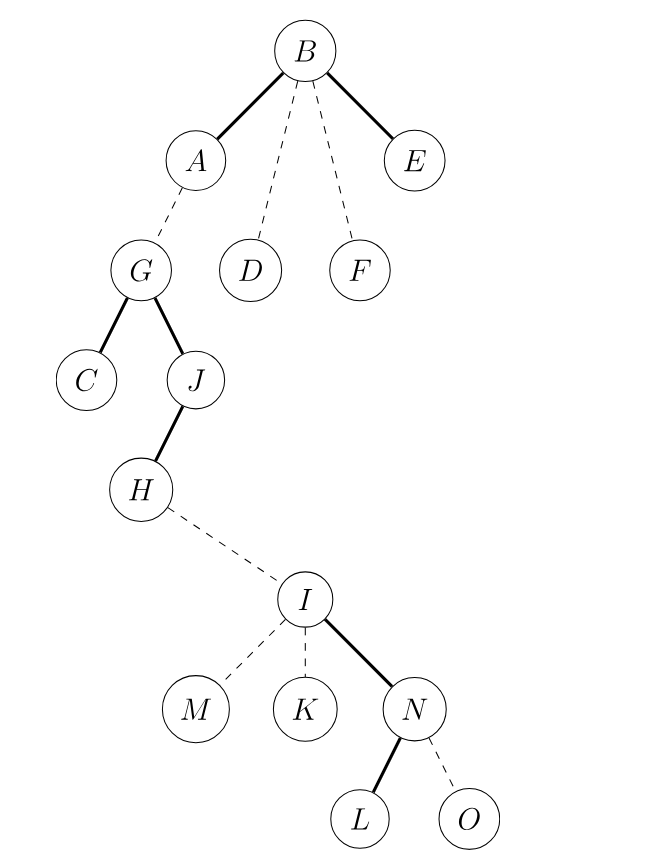
// 回顾一下代码
int access(int x)
{
int y;
for(y=0;x;y=x,x=tree[x].fa){
splay(x);
tree[x].ch[1] = y;
pushup(x);
}
return y;
}
我们发现 Access() 其实很容易,只有如下四步操作:
- 把当前节点转到根。
- 把儿子换成之前的节点。
- 更新当前点的信息。
- 把当前点换成当前点的父亲,继续操作。
这里提供的 Access 还有一个返回值。这个返回值相当于最后一次虚实链变换时虚边父亲节点的编号。该值有两个含义:
- 连续两次 Access 操作时,第二次 Access 操作的返回值等于这两个节点的 LCA.
- 表示 到根的链所在的 Splay 树的根。这个节点一定已经被旋转到了根节点,且父亲一定为空。
makeRoot()
Make_Root()的重要性丝毫不亚于Access()。我们在需要维护路径信息的时候,一定会出现路径深度无法严格递增的情况,根据 AuxTree 的性质,这种路径是不能出现在一棵 Splay 中的。- 这时候我们需要用到
Make_Root()。 Make_Root()的作用是使指定的点成为原树的根,考虑如何实现这种操作。- 设
Access(x)的返回值为 ,则此时 到当前根的路径恰好构成一个 Splay,且该 Splay 的根为 . - 考虑将树用有向图表示出来,给每条边定一个方向,表示从儿子到父亲的方向。容易发现换根相当于将 到根的路径的所有边反向(请仔细思考)。
- 因此将 到当前根的路径翻转即可。
- 由于 是 到当前根的路径所代表的 Splay 的根,因此将以 为根的 Splay 树进行区间翻转即可。
void makeroot(int x)
{
x = access(x);
swap(tree[x].ch[0],tree[x].ch[1]);
tree[x].tag^=1;
}
findroot()
- 查找的是 所在的 原树 的根,请不要把原树根和辅助树根弄混。在
Access(p)后,再Splay(p)。这样根就是树里深度最小的那个,一直往左儿子走,沿途PushDown即可。 - 一直走到没有 ls,非常简单。
- 注意,每次查询之后需要把查询到的答案对应的结点
Splay上去以保证复杂度。
int findroot(int x){
access(x);
splay(x);
while(tree[x].ch[0])pushdown(x),x=tree[x].ch[0];
splay(x);
return x;
}
Link()
- Link 两个点其实很简单,先
Make_Root(x),然后把 的父亲指向 即可。显然,这个操作肯定不能发生在同一棵树内,所以记得先判一下。
void link(int x,int y)
{
makeroot(x);
if(findroot(y)!=x){
splay(x);
tree[x].fa = y;
}
}
Split()
Split操作意义很简单,就是拿出一棵 Splay,维护的是 到 的路径。- 先
MakeRoot(x),然后Access(y)。如果要 做根,再Splay(y)。 - 另外 Split 这三个操作可以直接把需要的路径拿出到 的子树上,可以进行其他操作。
void split(int x,int y)
{
makeroot(x);
access(y);
splay(y);
}
Cut()
Cut有两种情况,保证合法和不一定保证合法。- 如果保证合法,直接
Split(x, y),这时候 是根, 一定是它的儿子,双向断开即可。就像这样:
void cut(int x,int y)
{
makeroot(x);
if(findroot(y)==x && tree[y].fa==x && tree[y].ch[0]==0){
tree[x].ch[1] = 0;
tree[y].fa = 0;
pushup(x);
}
}
如果是不保证合法,我们需要判断一下是否有,这里选择使用 map 存一下,但是这里有一个利用性质的方法:
想要删边,必须要满足如下三个条件:
- 连通。
- 的路径上没有其他的链。
- 没有右儿子。
总结一下,上面三句话的意思就一个: 之间有边。
具体实现就留作一个思考题给大家。判断连通需要用到后面的 Find,其他两点稍作思考分析一下结构就知道该怎么判断了。
注意事项
- 操作前一定要想一想需不需要
PushUp或者PushDown,LCT 由于特别灵活的原因,少Pushdown或者Pushup一次就可能把修改改到不该改的点上! - LCT 的
Rotate和 Splay 的不太一样,if (z)一定要放在前面。 - LCT 的
Splay操作就是旋转到根,没有旋转到谁儿子的操作,因为不需要。
